Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

Author: Jun-Yan Zhu∗, Taesung Park∗, Phillip Isola, Alexei A. Efros
Date: Mar 30, 2017
URL: https://arxiv.org/abs/1703.10593

Introduction

• Image-to-image translation 은 paired data의 상황에서 많이 연구.
• 하지만 실제 환경에선 이런 paired data를 구하기 힘듦.
• 본 논문은 unpaired data 상황에서 Network가 image-to-image 를 잘 학습하는 것에 초점을 맞춤.

Formulation

• \(X, Y\): X, Y 도메인의 데이터
• \(G, F\): X to Y generator, Y to X generator
• \(D_X, D_Y\): X, Y 도메인에 대한 Discriminator

Adversarial Loss

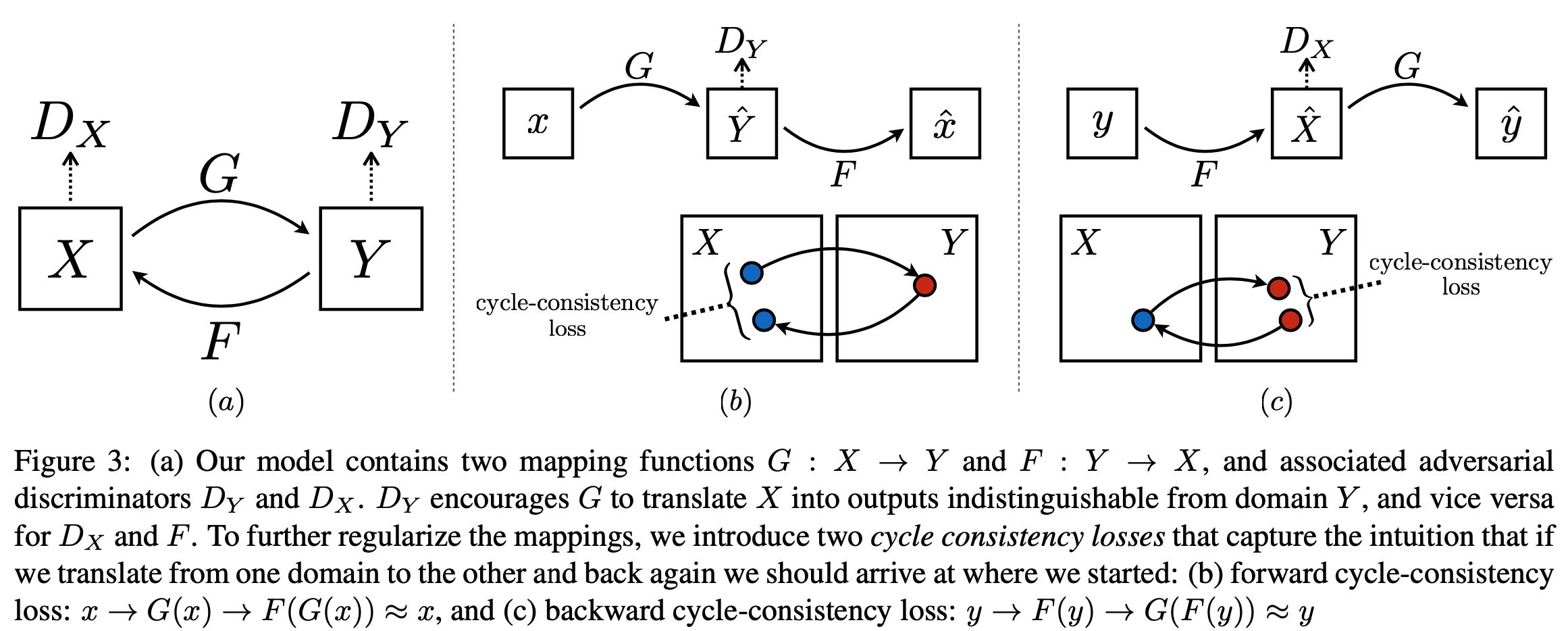
$$\mathcal{L}_{GAN}(G, D_Y, X, Y) = \mathbb{E}_{y\sim p_{data}(y)}[\log D_Y(y)] + \mathbb{E}_{x\sim p_{data}(x)}[\log (1 - D_Y(G(x)))]$$

$$\mathcal{L}_{GAN}(F, D_X, Y, X) = \mathbb{E}_{x\sim p_{data}(x)}[\log D_X(x)] + \mathbb{E}_{y\sim p_{data}(y)}[\log (1 - D_x(F(y)))]$$

Cycle Consistency Loss

• 각각의 X, Y 데이터를 Y, X 데이터로 변환 후 다시 X, Y 데이터 복원.

$$\mathcal{L}_{cyc}(G, F) = \mathbb{E}_{x\sim p_{data}(x)}[||F(G(x)) - x||_1 + \mathbb{E}_{y\sim p_{data}(y)}[||G(F(y)) - y||_1$$

Full Objective

$$\mathcal{L}(G, F, D_X, D_Y) = \mathcal{L}_{GAN}(G, D_Y, X, Y) + \mathcal{L}_{GAN}(F, D_X, Y, X) + \lambda\mathcal{L}_{cyc}(G, F)$$

$$G^*,F^* = argmin_{G, F}argmax_{D_X, D_Y}\mathcal{L}(G, F, D_X, D_Y)$$

Implementation

Network Architecture

• Generator에서 Instance Normalization 사용.
• PixelGAN이 아닌 70x70 PatchGAN 사용.

Training detail

• Loss 에서 \(\lambda\) 는 10.
• Optimizer: Adam
• Learning rate: 0.002

Result

P.S

• Cycle consistency가 매우 신박
• Image translation 에선 Instance Normalization !