EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks
Author: Mingxing Tan, Quoc V. Le
Date: May 28, 2019
URL: https://arxiv.org/abs/1905.11946
Introduction
- ConvNet 의 성능을 높이는데 Depth, Width, Image size 중 하나를 증가 시키는게 일반적인 방법.
- 본 논문에서는 ConvNet의 성능과 효율성을 증가시키기 위한 원론적인 방법에 대한 연구.
- 실험의 결과로 Compound scaling method 를 제안.
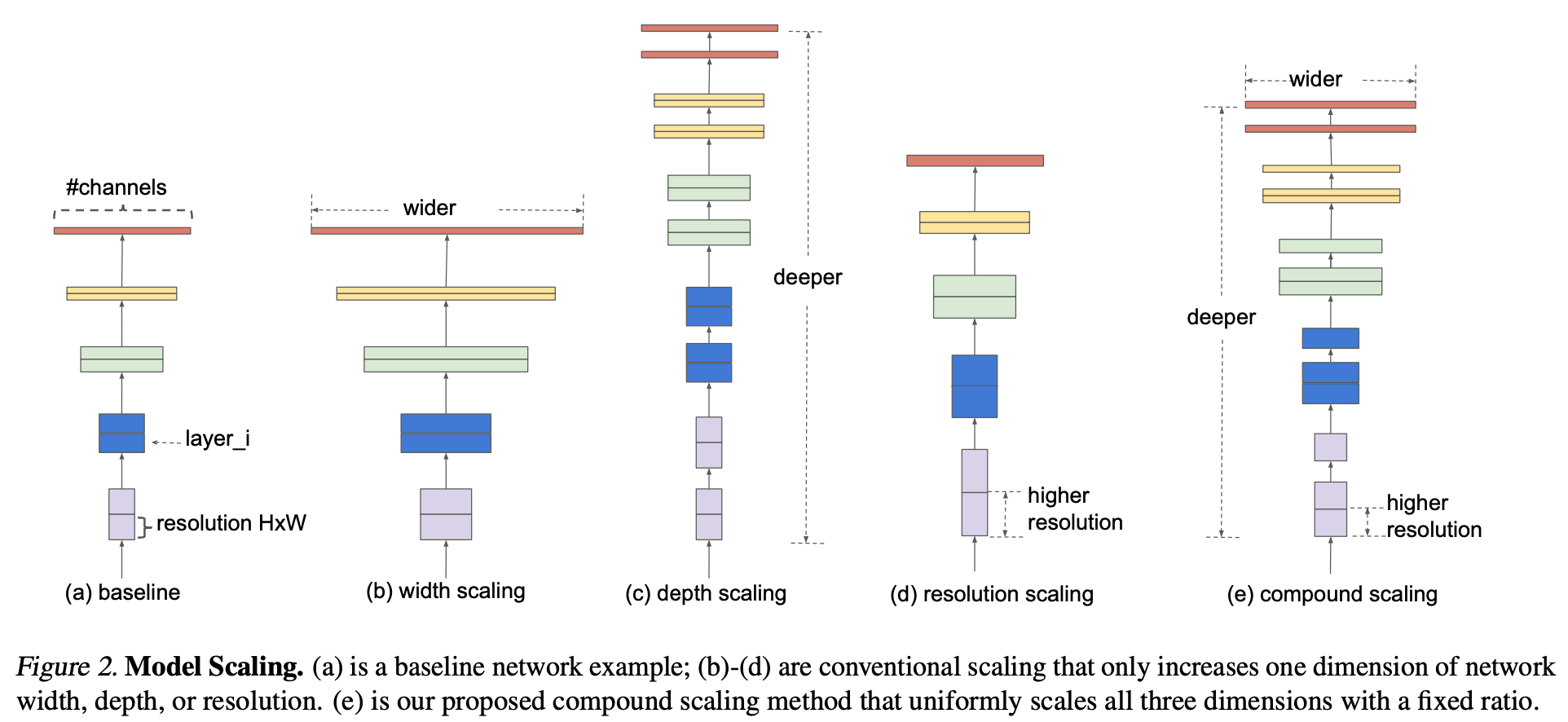
image
Compound Model Scaling
- Scaling 문제에 대한 정의, Approache 별 연구, 새로운 방법에 대한 내용 서술.
- Model scaling은 Baseline 에서 Length(Depth), Width, Resolution 를 확장.
- 하지만 실제론 리소스에 제약이 있으니 이에 맞춰 문제를 새롭게, 단순하게 정의.
- Design space를 줄이기 위해 모든 레이어는 상수 값을 이용하여 규칙적으로 변화하도록 함.
- 최종 목적은 제한된 리소스에서 성능을 최대화하는 것.
$$\mathcal{N}: \text{ConvNet}$$
$$ \mathcal{F}_i: \text{Layer architecture}$$
$$L_i: \text{Network length}$$
$$C_i: \text{Width}$$
$$H_i, W_i: \text{Input resolution}$$
$$
{max}_{d, w, r} \space\space\space\space Accuracy(\mathcal{N}(d, w, r))
$$
$$s.t. \space\space\space\space \mathcal{N}(d, w, r) = \bigodot_{i=1…s}\hat{\mathcal{F}}_i^{d \cdot \hat{L}i}(X{\langle r\cdot \hat{H}_i, r \cdot \hat{W}_i, w\cdot \hat{C}_i \rangle} )$$
$$Memory(\mathcal{N}) \leq \text{target memory}$$
$$FLOPS(\mathcal{N}) \leq \text{target flops}$$
Scaling Dimensions
- 두번째 문제는 d, w, r 이 서로 dependent 하고 제한된 리소스에 따라 값이 변화.
- 그래서 기존에는 다음 세 개의 요소 중 하나를 변경함.
Depth (d)
- VGGNet, GoogLeNet, ResNet 등등 레이어를 많이 많이 !
Width (w)
- 채널 수를 늘리고 깊이를 줄이는 방식.
- 하지만 higher level feature를 잡기 힘들 수 있음.
Resolution (r)

image
- Observation 1: 이를 통해서 어떤 요소를 증가시키던 성능이 오르는 것을 확인 하지만 Model이 무거워짐.
Compound Scaling
- 경험적으로 세 요소가 dependent 하다는 것을 이미 알고 있음.
- 다른 depth, resolution 을 이용하여 성능 비교.
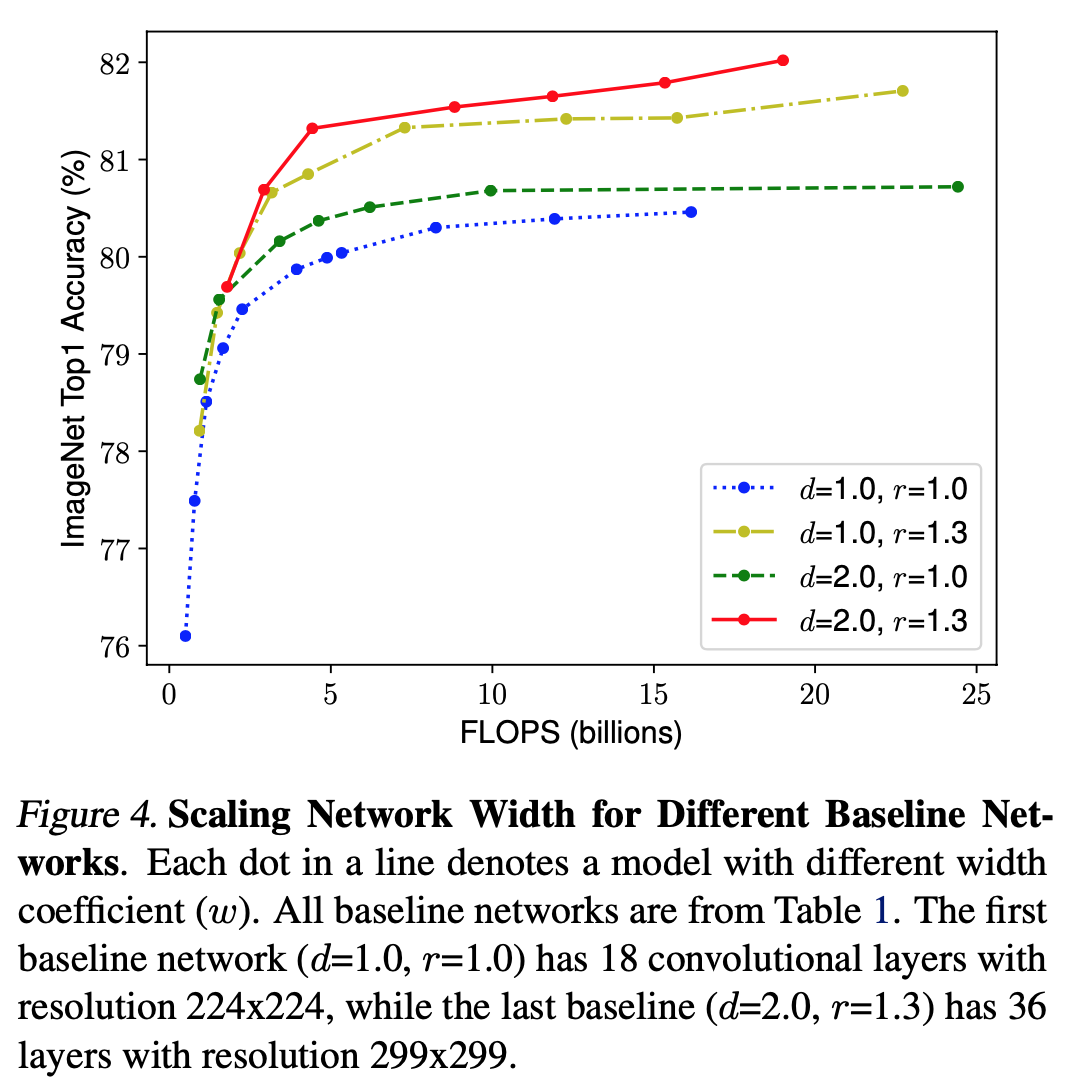
image
- Observation 2: 세 요소의 balance가 매우 중요..
- 다음과 같은 compound scaling method 제안.
$$\phi: \text{Compound Coefficient} \\ depth: d = \alpha^\phi \\ width: w = \beta^\phi \\ resolution: r = \gamma^\phi \\ \text{s.t. }\alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \\ \alpha \ge 1, \beta \ge 1, \gamma \ge 1$$
- 각 값은 small grid search로 결정된 상수 값.
EfficientNet Architecture
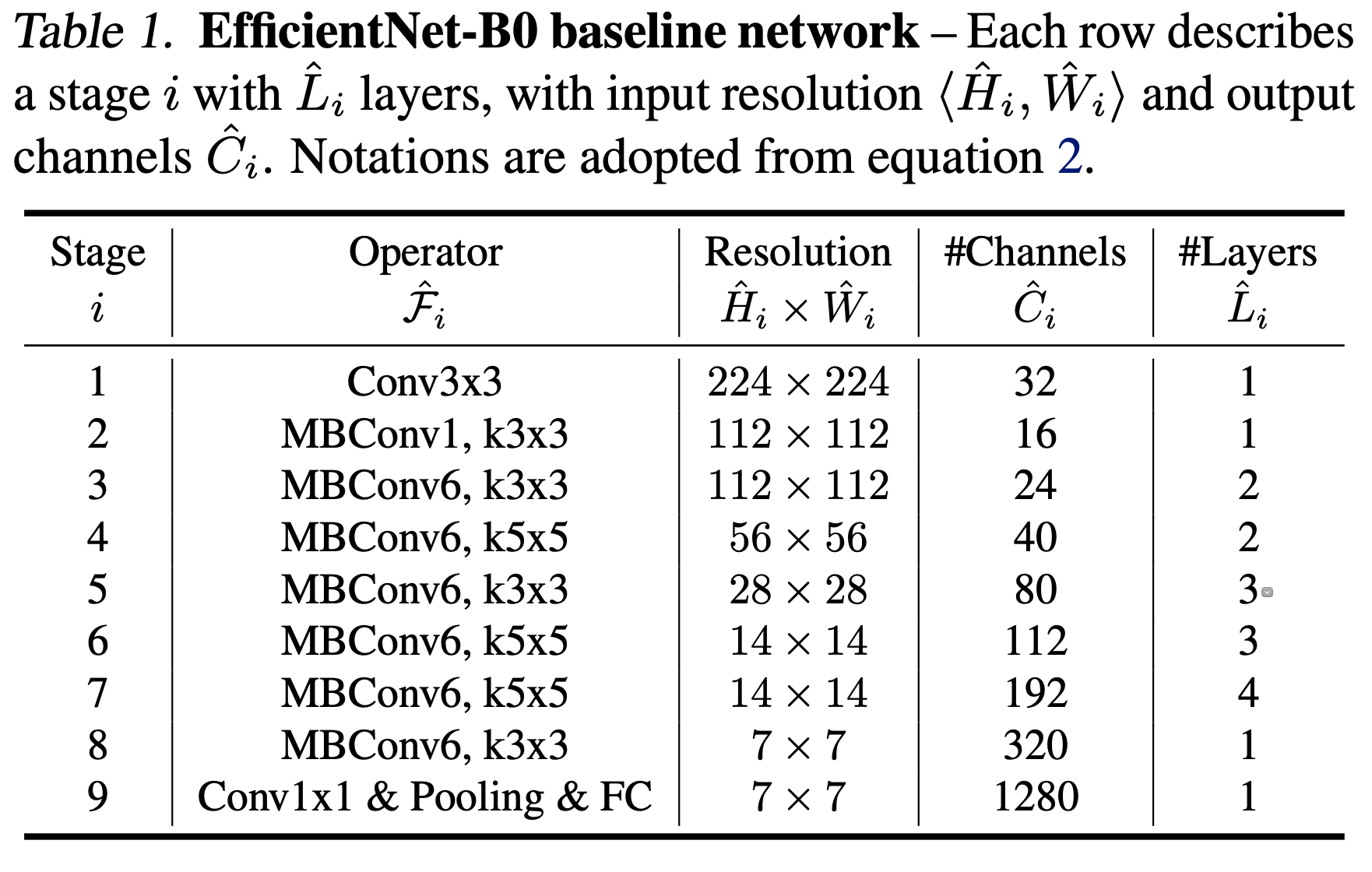
image
- EfficientNet-B0 를 baseline network로 하여 Accuracy, FLOPS 둘 다 최적화하도록 multi-objective neural architecture search 적용.
- Step 1
- \(\phi\) =1 로 고정
- 식 2, 3을 기반으로 하여 small grid search
- EfficientNet-B0에 가장 적합한 값을 \(\alpha=1.2, \beta=1.1, \gamma=1.15\)
- Step 2
- \(\alpha, \beta, \gamma\)를 고정하고 \(\phi\)를 변경하여 실험.
- Result (ImageNet Result for EfficientNet) 참고
Result
Scaling Up MobileNets and ResNets
- Compound scale 을 증명하기 위해 MobileNet과 ResNet을 이용하여 비교.
- 기존의 방법들은 3개중 1개의 요소만 scaling.

image
ImageNet Result for EfficientNet
-
Training Setting
- Optimization
- RMSProp
- Decay: 0.9
- Momentum: 0.9
- Batch normalization
- Weight decay: 1e-5
- Initial learning rate: 0.256
- Decay: 0.97 (every 2.4 epochs)
- Swish Activation
- AutoAugmentation: 뭔지 모르겠군 1
- Stochastic depth: 뭔지 모르겠군 2
- Dropout
-
B0부터 B7 까지 성능 비교.
-
GPipe에 비해 8.4배 적고 좋은 성능.
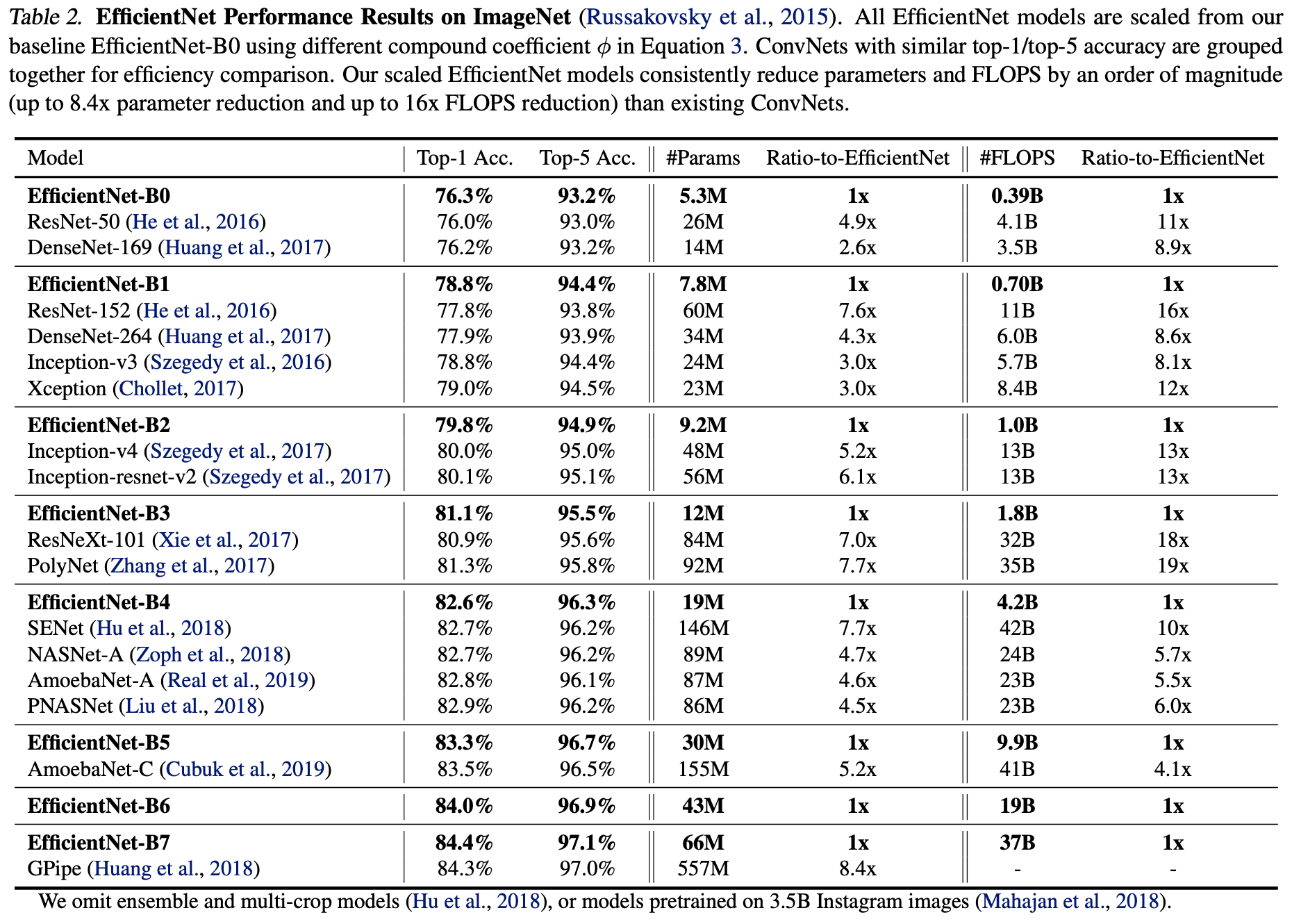
image
- CPU를 이용한 Inference 속도 비교.

image

image
Transfer Learning Result for EfficientNet
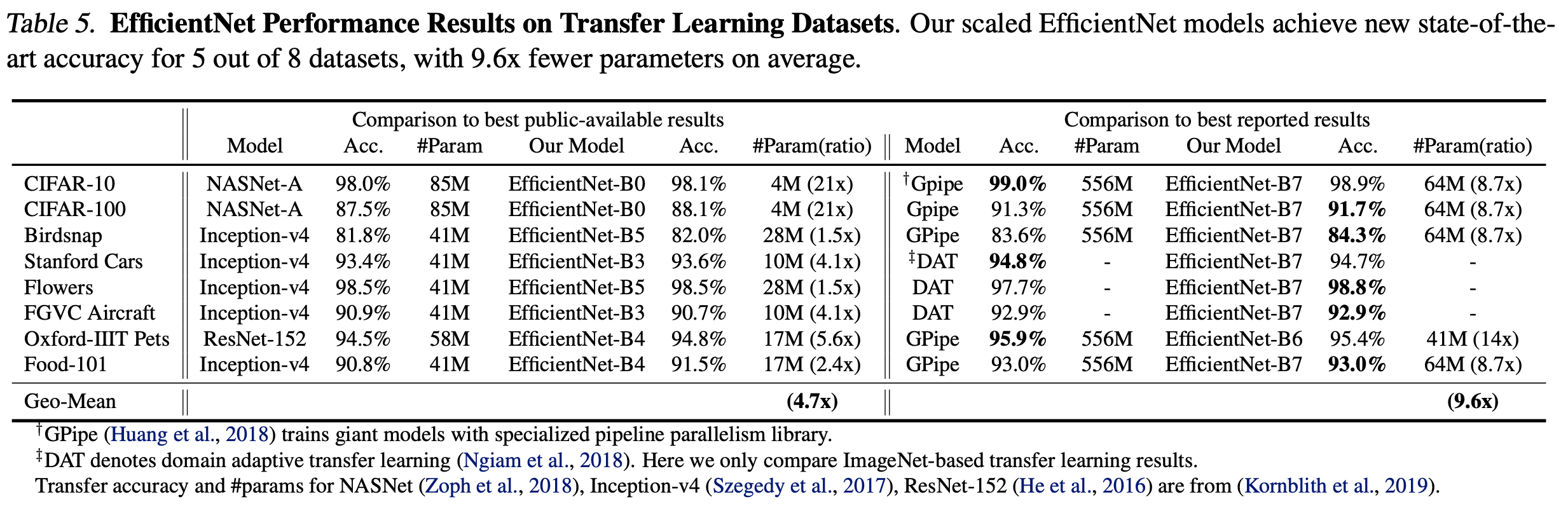
- ImageNet pretrained model 을 이용하여 각종 Dataset을 Transfer learning 한 성능 비교
- 사용한 Dataset

image
- Transfer learning 결과
- 전체적으로 모델이 가벼움.
image
- 기존의 모델들과 비교하여 가볍지만 뛰어난 성능을 보임.
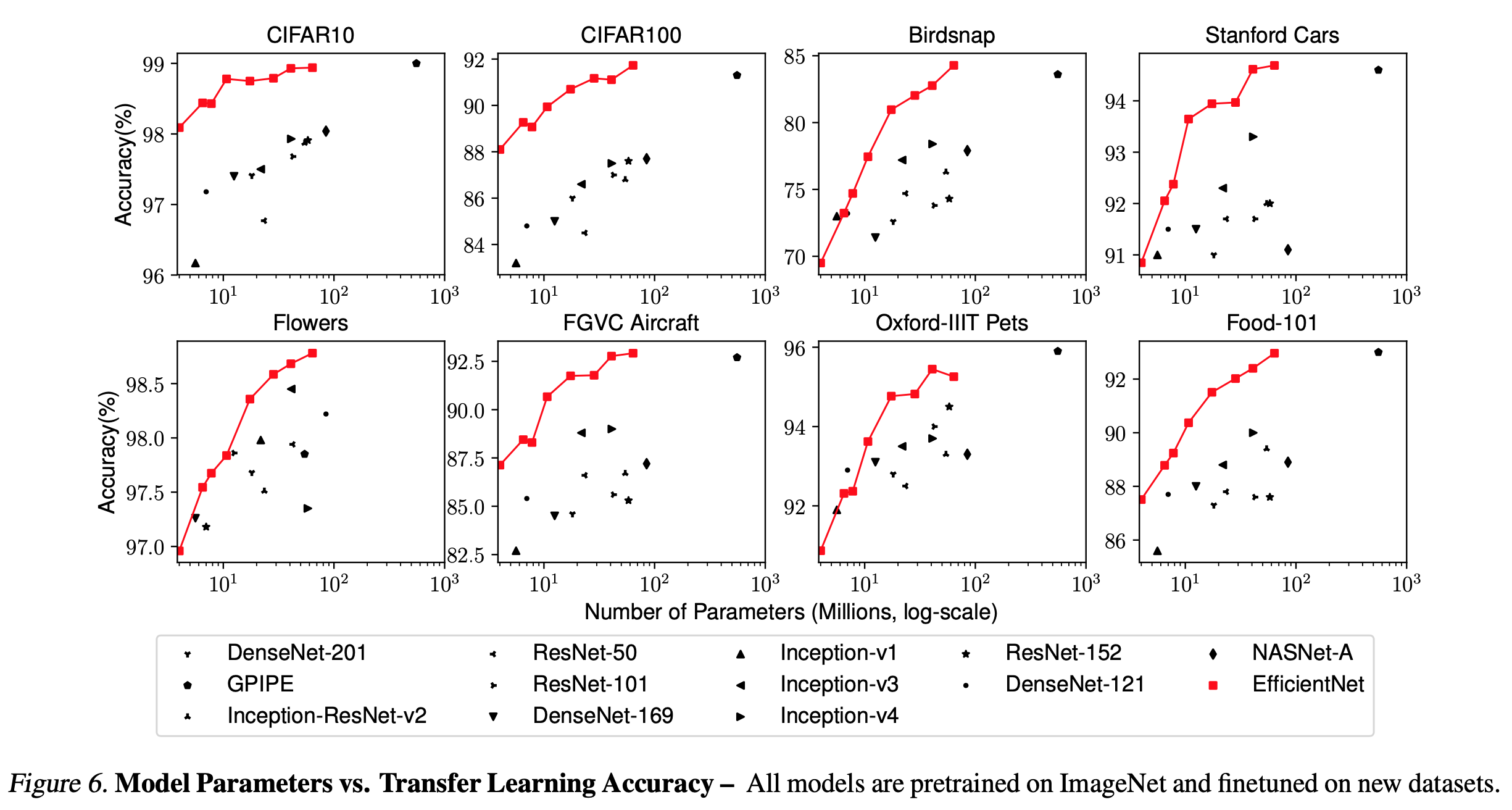
image
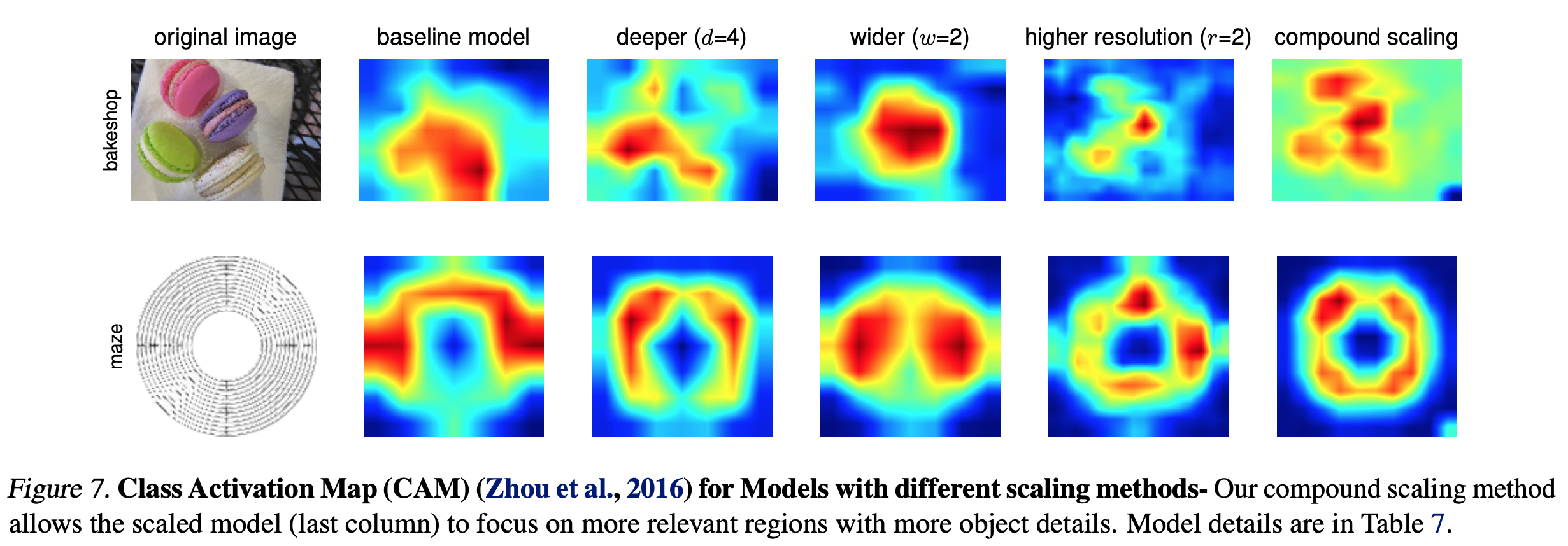
Discussion
- EfficientNet-B0 를 이용하여 각기 다른 scaling method를 이용하여 성능 비교

image
image

image
P.S
- 이런 연구는..NAS(Network Architecture Search)가 답..인건가
- 근데 이것도 하드웨어가 빵빵해야….. 크흡















