StarGAN: Unified Generative Adversarial Networks for Multi-Domain Image-to-Image Translation

Author: Yunjey Choi, Youngjung Uh, Jaejun Yoo, Jung-Woo Ha
Date: Dec 21, 2019
URL: https://arxiv.org/abs/1711.09020

Introduction

• Multi domain image translation 이라고 하면 다음 사진과 같이 머리 색, 성별, 연령대 등과 같이 여러 condition 에 대응하는 영상을 생성.

• 기존의 image-to-image translation 은 n개의 domain 을 적용할 시에 n*(n-1) 개의 generator가 필요했음.
• StarGAN은 한 1개의 generator로 n개의 domain 을 적용.

Star Generative Adversarial Networks

Loss functions

• Adversarial Loss

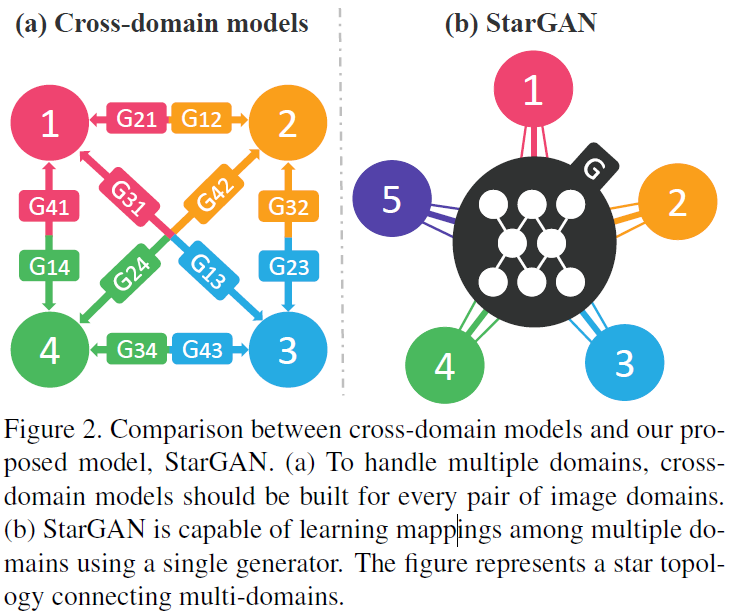
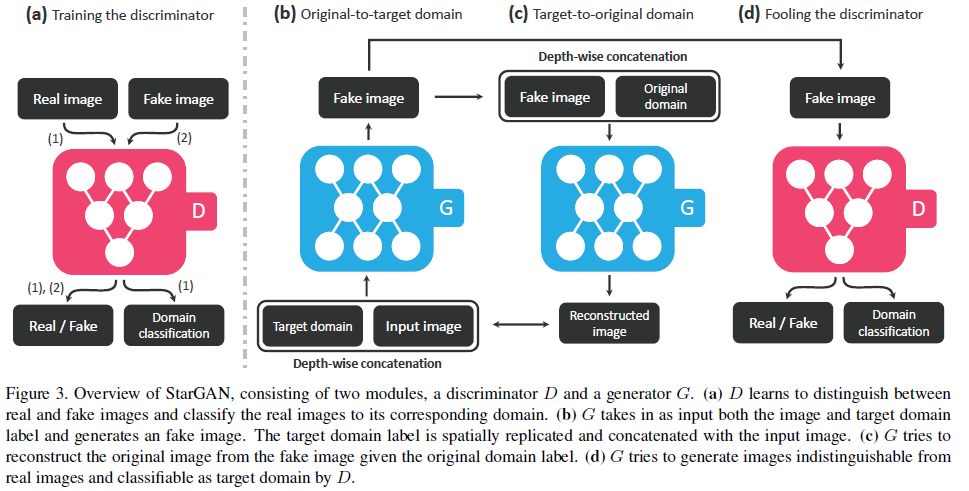
$$\mathcal{L}_{adv} = \mathbb{E}_x [\log D_{src}(x)] + \mathbb{E}_{x, c} [\log (1-D_{src}(G(x,c)))] - \lambda_{gp}\mathbb{E}_{\hat{x}}[(\Vert \nabla_{\hat{x}}D_{src}(\hat{x})\Vert_2 -1)^2]$$

$$\lambda_{gp} = 10$$

• Domain Classification Loss

$$\mathcal{L}^r_{cls} = \mathbb{E}_{x, c'}[-\log D_{cls}(c'|x)]$$

$$\mathcal{L}^f_{cls} = \mathbb{E}_{x, c'}[-\log D_{cls}(c|G(x, c)]$$

• Reconstruction Loss

$$\mathcal{L}_{rec} = \mathbb{E}_{x, c, c'}[\Vert x-G(G(x, c), c')\Vert_1]$$

• Full Objective

$$\mathcal{L}_D = -\mathcal{L}_{adv} + \lambda_{cls}\mathcal{L}^r_{cls}$$

$$\mathcal{L}_G = \mathcal{L}_{adv} + \lambda_{cls}\mathcal{L}^f_{cls}+\lambda_{rec}\mathcal{L}_{rec}$$

$$\lambda_{cls} = 1, \lambda_{rec} = 10$$

Result

Training Detail