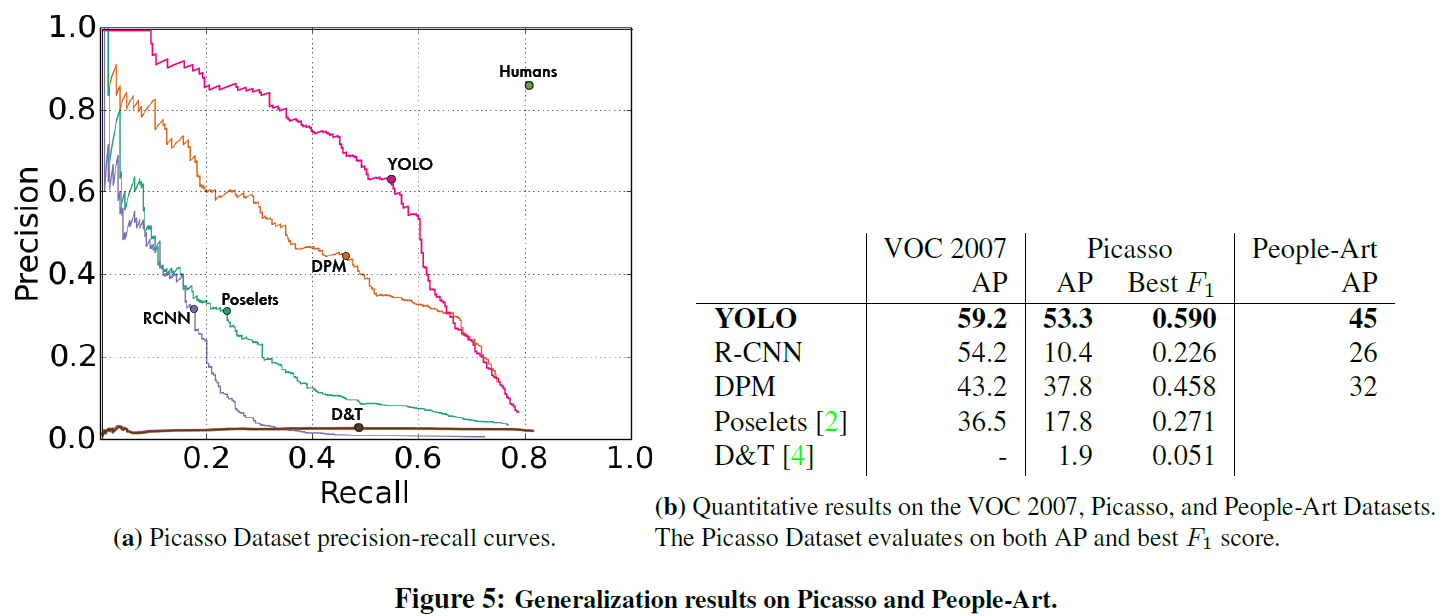
You Only Look Once: Unified, Real-Time, Object detection

편의상 bounding box -> bbox

Abstract

Object detection을 bboxes, class probabilities regression 문제로 접근.
Single Neural Network 로 bboxes와 class probabilities 둘 다 예측.
Localization Error가 다소 높지만 background error가 낮음.
End-to-End, Extremely fast

1. Introduction

Current Detection 시스템
- DPM : Sliding Window 방식
- R-CNN 계열 : potential bboxes 추출 -> image 에서 bboxes 부분 다시 classify -> Post-processing
Slow, Hard to optimize(각 요소별로 따로따로 학습을 해야함. RPN -> Classifier -> RPN -> …)

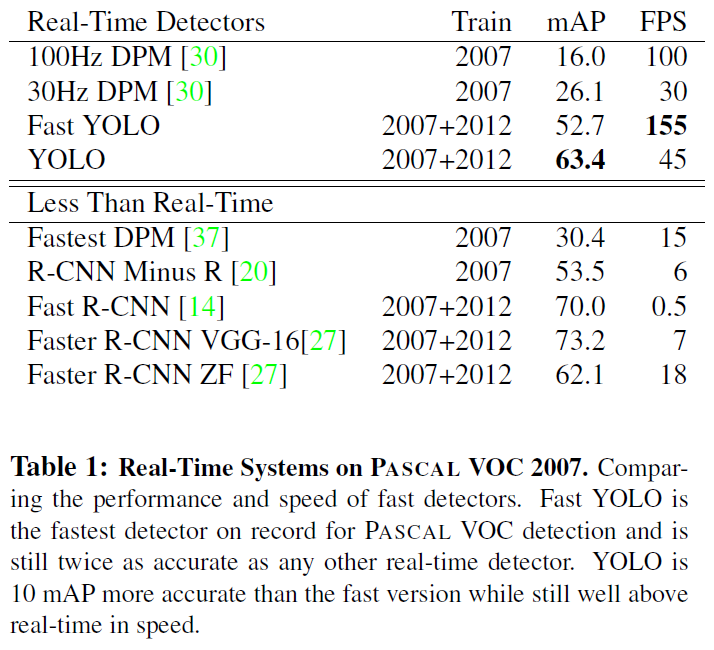
복잡하지 않은 pipeline과 빠른 inferenc time.
- 45 fps on a Titan X .
이미지 전체를 이용한 prediction
- Fast R-CNN 보다 적은 background error
Object의 general한 representations 학습.
- natural image로 학습하고 art works로 test 했을 때 기존의 DPM 이나 R-CNN 보다 성능이 좋았다.
- 새로운 도메인이나 뭔가 모를 입력에 대해 일반화 할 수 있다.

2. Unfied Detection

Single Neural Network로 통합.
이미지 전체를 이용해서 각각의 bbox 예측.

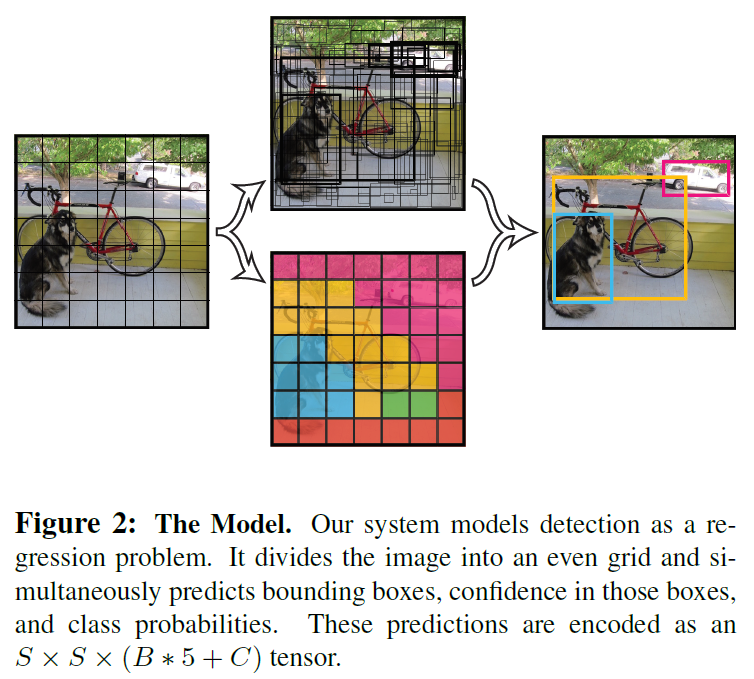
입력 이미지를 S x S grid로 나눔.
- Feature map이 S x S 라고 이해하면 됨.
각 grid cell은 B개의 bbox의 정보(x, y, w, h, confidence score), 해당 grid cell의 Class probabilities 정보를 가짐.
- bbox의 정보
  - x, y : bbox의 center 좌표
  - w, h : 이미지 크기에 대비한 상대적인 값.
  - confidence score : bbox가 object를 가졌는지 box가 얼마나 정확히 예측했는지에 대한 score
  - Confidence Score는 다음과 같이 정의. $${Confidence; Score}= Pr(Object) * IOU^{truth}_{pred}$$
  - No object의 경우
    - Confidence Score는 0 이어야함.
  - Confidence Score가 IOU와 같아지길 원함.
- Class Probabilities 정보
  - C개의 class에 대한 conditional class probabilities, $Pr(Class_i \mid Object)$
  - Test 시에는 Conditional class probabilities와 individual box confidence score를 곱했다고 함.
    $Pr(Class_i|Object) = Pr(Object) * IOU^{truth}_{pred} = Pr(Class_i) * IOU^{truth}_{pred}$
  - bbox 별로 class confidence score를 알 수 있음.
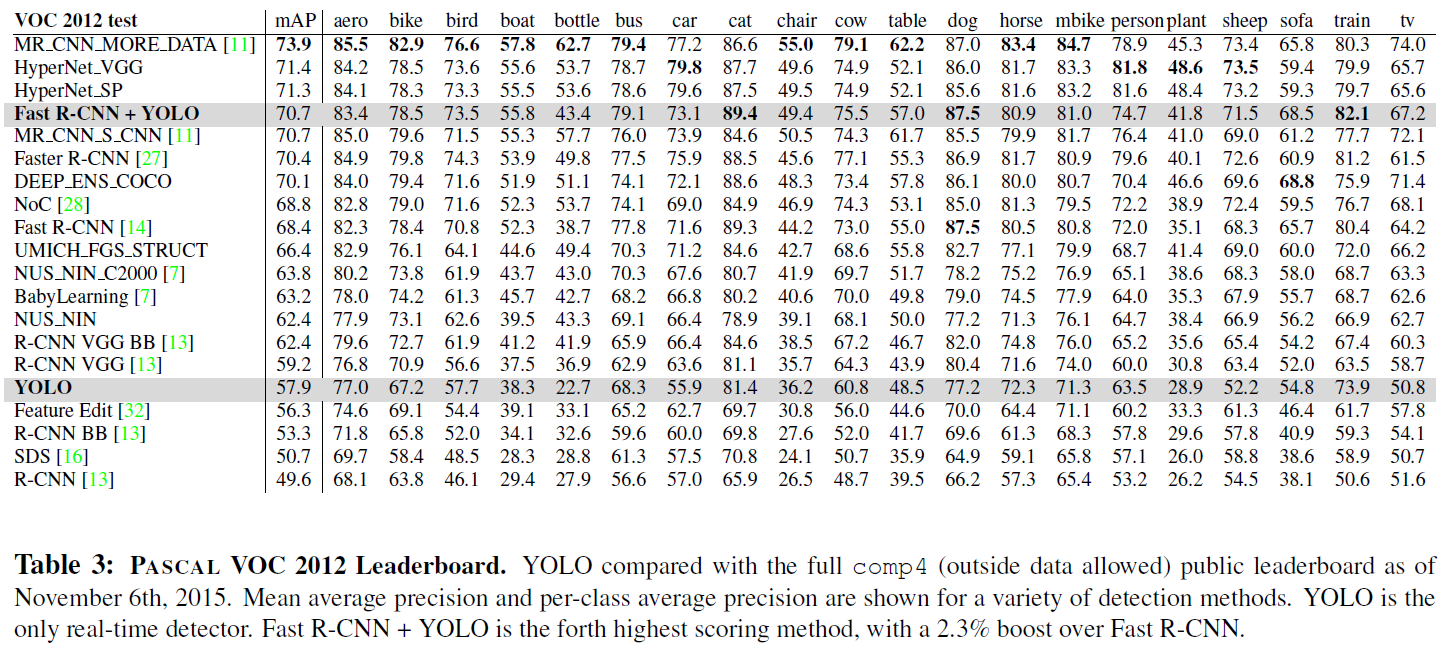
PASCAL VOC 로 평가. S = 7, B = 2, C = 20
최종 출력은 7 x 7 x 30 의 tensor.

2.1 Design

24개의 Convolution layer, 2개의 Fully Connected layer.
GoogLeNet의 inception 모듈 대신에 1 x 1 Convolution layer를 이용하여 reduction.
Tiny model은 9개의 Convolution layer, 2개의 Fully Connected layer.

2.2 Training

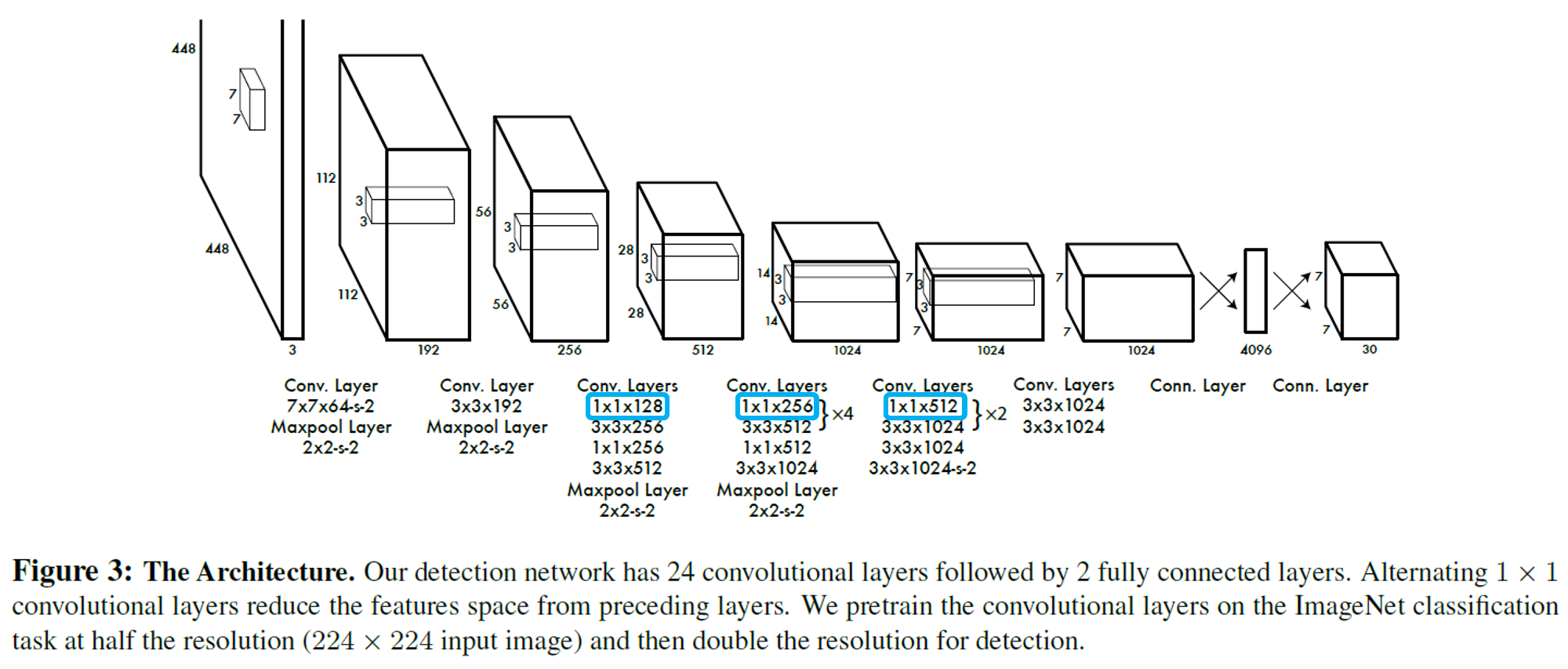
앞 단의 20개의 Convolution layer(Feature Extractor)를 ImageNet 1000-class competition 데이터(224 x 224)로 Pretrain.
20번째 Convolution layer 뒤에 Average Pooling, Fully Connected Layer.
ImageNet 2012 validation set으로 top-5 accuracy 88% 정도..
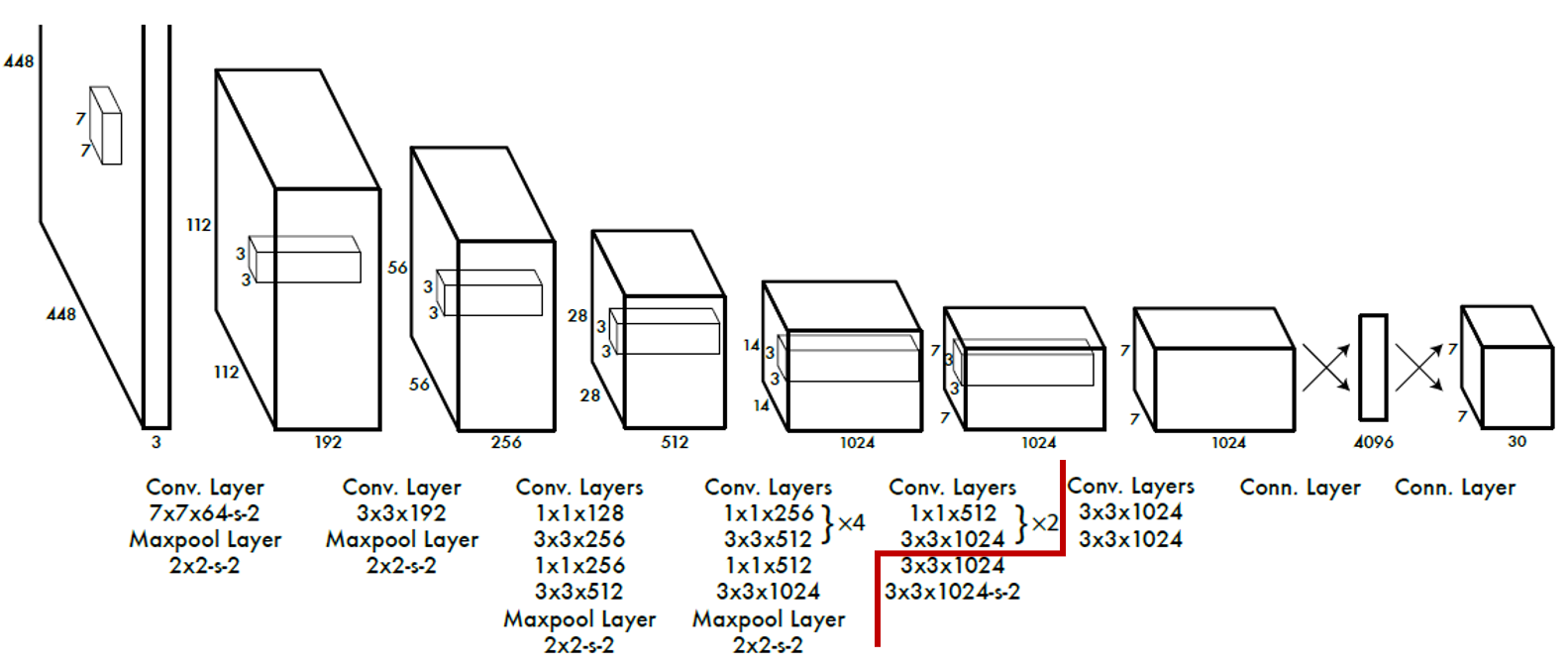
Pretrain 후 Detector 부분 추가 후 입력 크기를 448 x 448 로 높여서 학습 진행.
Bounding Box의 width, height 값은 이미지의 width, height로 normalize 하여 0 ~ 1 사이 값을 같도록 함.
Bounding Box의 x, y 값은 특정 grid cell의 left top으로부터 offset 값. 0 ~ 1 사이 값을 같도록 함.
마지막 layer는 linear activation function 사용.
다른 layer는 leaky ReLU 사용. $$\phi(x)=\begin{cases}x,&if;x >0\\ {0.1}x, & otherwise\end{cases}$$
Optimization이 쉬운 Sum-Squared Error 를 사용.
이미지의 대부분 grid cell이 object 를 가지고 있지 않기 때문에 Confidence Score가 0 에 수렴.
이 상황에선 object를 가지고 있는 grid cell의 gradient를 압도할 수 있음.
이를 해결하기 위해 Bbox coordinate loss와 No object의 confidence loss 에 대해 weight 를 부여.
$\lambda_{coord} = 5$ and $\lambda_{noobj} = 0.5$.
Sum-Squared Error는 large boxes와 small boxes 를 동일하게 평가.
large boxes 에 대해서 중요성을 반영하기 위해 width, height 는 square root 사용.

$$\lambda_{coord}\sum^{S^2}_{i=0}\sum^B_{j=0}\mathbb{I}^{obj}{ij}(x_i-\hat{x}i)^2+(y_i-\hat{y}i)^2$$ $$+\lambda{coord}\sum^{S^2}_{i=0}\sum^B{j=0}\mathbb{I}^{obj}{ij}(\sqrt{w_i}-\sqrt{\hat{w}i})^2 + (\sqrt{h_i}-\sqrt{\hat{h}i})^2$$ $$+ \sum^{S^2}_{i=0}\sum^B{j=0}\mathbb{I}^{obj}{ij}(C_i - \hat{C}i)^2$$ $$ + \lambda{noobj}\sum^{S^2}_{i=0}\sum^B_{j=0}\mathbb{I}^{noobj}_{ij}(C_i - \hat{C}i)^2 $$ $$ + \sum^{S^2}_{i=0}\mathbb{I}^{obj}_{i}\sum^B{c\in{classes}}(p_i(c) - \hat{p}_i(c))^2 $$

$\mathbb{I}^{obj}_{i}$ : Object가 존재하는 Grid Cell i.
$\mathbb{I}^{obj}_{ij}$ : Object가 존재하는 Grid Cell i의 Bounding Box j.
Train 관련 Parameter
- Batch Szie : 64
- Momentum : 0.9
- Decay : 0.0005
- Learning rate
  - $10^{-3}$ 부터 $10^{-2}$ 까지 천천히 증가.
  - $10^{-2}$ 로 75 epochs 학습.
  - $10^{-3}$ 로 줄여서 30 epochs 학습.
  - $10^{-4}$ 로 줄여서 30 epochs 학습.
- Dropout : 0.5
- Data Augmentation
  - Random Scaling, Translation of up to 20% of the original image size.
  - Random adjustment exposure and saturation

2.3 Inference

Large Object 나 여러 grid cell에 걸쳐있는 object는 여러 셀에 predict 될 수 있음.
Non-maximal suppression 사용하여 해결.

2.4 Limitations of YOLO

각 Grid Cell은 하나의 클래스만 가질 수 있기 때문에 Grid Cell 하나에 작은 object가 여러 개 있을때 제대로 예측하지 못할 수 있다.
예상치 못한 aspect ratio나 configuration을 가진 객체를 일반화 하는데 어려움.
Large box와 Small box를 동일하게 처리.
Large box의 small error보다 Small box의 small error가 IOU에 훨씬 큰 영향을 끼침.